Mesoscopic wave physics with a dense school of fish in a sea farm cage

Wave scattering in disordered media is an interdisciplinary subject of great practical importance in such areas of science as condensed matter physics, optics, seismology, medical imaging, etc. In many situations, different types of waves (“Schrödinger waves” describing quantum particles, light, sound, seismic waves, etc.) exhibit very similar behavior when they propagate in a randomly inhomogeneous, disordered media. Of special interest are the so-called mesoscopic phenomena that originate from interferences of scattered waves, which are made possible by the phase coherence that the waves preserve despite the disorder. Mesoscopic phenomena in wave scattering are vital for many practical applications, such as the modern miniaturized electronics, medical and seismic imaging, and nondestructive testing of industrially important materials.

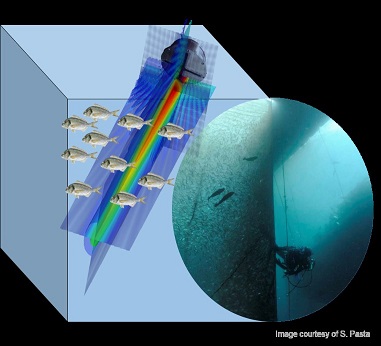
Here we propose to study the multiple scattering of ultrasound by a dense school of fish confined in a large sea farm cage. It turns out that fishes can scatter sound very strongly, allowing one to achieve a scattering mean free path (= a distance between successive scattering event) comparable with the wavelength of ultrasound.

The strong scattering allows us to observe such mesoscopic phenomena as the coherent backscattering, field and intensity correlations, fluctuations of the local density of states, etc. and motivates the first objective of this thesis proposal: a study of mesoscopic interference effects in multiple scattering from the wavefield recorded on a 3D ultrasonic array. On the other hand, we propose to use the statistical properties of the scattered ultrasound to probe and monitor the behavior of fishes in a large school. This second objective of the thesis proposal is motivated by potential applications in the science of animal behavior and in the aquaculture industry.

The spatial and temporal correlations of scattered ultrasound contain information about the size and the number of fishes in the tank, as well as about their collective motion. Extracting this information is a formidable inverse problem that we aim to solve.